前向投影的解析计算
要求
编写实现扇形束或平行束CT前向投影解析计算的代码,获取Shepp Logan仿体的前向投影, 并显示对应的sinogram图;将Shepp Logan修改为一个非常小的点源,采用前向投影解析计算的代码,计算该点源的Sinogram图并显示。
注意:Shepp Logan仿体定义有很多变体,实现是选取其中一个即可。
思路
前向投影的解析计算方法,计算对应图像的每一个点投影到探测器对应位置,统计每个角度每个探测器上的数值。
可以通过两步进行计算:
(1)根据探测器角度与探测器编号计算对应探测器的直线方程,该直线从探测器上一点到图像;
(2)计算该直线方程穿过的椭圆长度,并结合椭圆强度值,计算穿过的所有椭圆长度乘强度之和作为该探测器的接收值;
通过两个函数分别实现:
CalSlope():对直线方程的计算;
CalDis3():统计探测器接收的信号;
Sheep Logan仿体
使用椭圆函数定义的方法构建Sheep-Logan图像
% 强度 半长轴 半短轴 位置x 位置y 倾斜度
ellipse = [ 1 .69 .92 0 0 0
-.8 .6624 .8740 0 -.0184 0
-.2 .1100 .3100 .22 0 -18
-.2 .1600 .4100 -.22 0 18
.1 .2100 .2500 0 .35 0
.1 .0460 .0460 0 .1 0
.1 .0460 .0460 0 -.1 0
.1 .0460 .0230 -.08 -.605 0
.1 .0230 .0230 0 -.606 0
.1 .0230 .0460 .06 -.605 0 ];
I = phantom(ellipse,256);
figure
imshow(I,[])

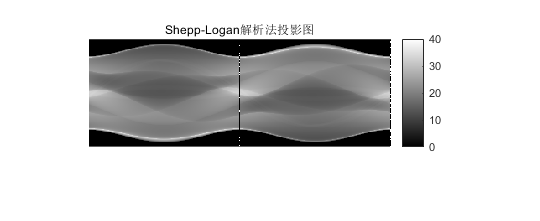
由投影结果可以看出,解析法在θ为0度和180度时出现比较明显的错误,原因是函数定义直线y = k*x + b。在探测器旋转过程中,当k = ∞时,直线函数变为x = a。
点源仿体
使用较小的圆
%点源参数(一个较小的圆)
point = [ 1 .01 .01 0 0.3 0 ];
I = phantom(point,256);
figure
imshow(I,[])


由投影结果可以看到,对于单个点源图像的计算由比较大的误差,其中部分角度缺失,投影质量较差。
代码
主程序
clc,clear
%shepp-logan模型的参数
% 强度 半长轴 半短轴 位置x 位置y 倾斜度
ellipse = [ 1 .69 .92 0 0 0
-.8 .6624 .8740 0 -.0184 0
-.2 .1100 .3100 .22 0 -18
-.2 .1600 .4100 -.22 0 18
.1 .2100 .2500 0 .35 0
.1 .0460 .0460 0 .1 0
.1 .0460 .0460 0 -.1 0
.1 .0460 .0230 -.08 -.605 0
.1 .0230 .0230 0 -.606 0
.1 .0230 .0460 .06 -.605 0 ];
%点源参数(一个较小的圆)
point = [ 1 .05 .05 0 0.3 0 ];
% 参数设定
NumDetector = 128; % 探测器数量
NumAngle = 360; % 旋转角度
ImgSize = [128,128]; % 设定图像大小
P = point;
I = phantom(P,256);
figure
imshow(I,[])
Rdata = zeros(NumDetector,NumAngle);
for i = 1:NumAngle
for j = 1:NumDetector
[k,b] = CalSlope(ImgSize,i,j,NumDetector);
tmp = 0;
for z = 1:size(P,1)
tmp = tmp + CalDis3(k,b,P(z,:),ImgSize(1));
end
Rdata(j,i) = tmp;
end
end
figure
imshow(Rdata,[0,40])
colorbar()
colormap(gray)
title("Shepp-Logan解析法投影图")
%title("Point解析法投影图")
函数
function [k,b] = CalSlope(ImgSize, angle, num, NumDetector)
% 本函数用于计算探测器在特定偏转角度,穿过特定探测晶体中心的直线方程
% Imgsize 图像大小
% angle 偏转角度
% num 晶体排序
% NumberDetector 晶体总数
DisAbord = 100;
%角度弧度制转换
anglePi = pi*angle / 180;
%计算k
%k1 = tan(anglePi);
if angle == 0
k = 1;
elseif angle == 90
k = 0;
else
k = -1/tan(anglePi);
end
%计算最中心的传感器的坐标
center_x = ImgSize(2)/2+sin(anglePi)*DisAbord;
center_y = ImgSize(1)/2-cos(anglePi)*DisAbord;
%算出第num个传感器距离中心的距离
DisCenter = (num-(NumDetector+1)/2);
%计算第num个传感器的坐标
x = center_x + DisCenter*cos(anglePi);
y = center_y + DisCenter*sin(anglePi);
%根据y=kx+b计算b
b = y - k*x;
end
function value = CalDis3(k_,b_,ellipse,width)
% 本函数用于计算直线穿过椭圆的长度
% k_ 直线斜率
% b_ 直线常量
% ellipse 以函数形式定义的椭圆
% width 图像宽度
% 椭圆参数
A = ellipse(1);
a = ellipse(2);
b = ellipse(3);
x0 = ellipse(4);
y0 = ellipse(5);
anglePi = pi*ellipse(6) / 180;
% 坐标系转换 (0,0)->(width/2,width/2)
b_= k_-1 + b_*2/width;
%将直线方程带入到旋转的椭圆方程中
% t2、t1、t0分别代表带入后的x的二次、一次以及常数项
k1 = cos(anglePi)+k_*sin(anglePi);
b1 = (b_-y0)*sin(anglePi)-x0*cos(anglePi);
k2 = k_*cos(anglePi)-sin(anglePi);
b2 = x0*sin(anglePi)+(b_-y0)*cos(anglePi);
t2 = b^2*k1^2+a^2*k2^2;
t1 = 2*b^2*k1*b1+2*a^2*k2*b2;
t0 = b^2*b1^2+a^2*b2^2-a^2*b^2;
delta = t1^2-4*t2*t0;
if delta<=0
value = 0;
else
x1 = (-t1-delta^0.5)/(2*t2);
x2 = (-t1+delta^0.5)/(2*t2);
y1 = k_*x1+b_;
y2 = k_*x2+b_;
value = ((x1-x2)^2+(y1-y2)^2)^0.5;
end
value = value*width/2*A;
end